
Harmonics and Superposition
In simple terms, the Fourier series breaks any periodic signal in one fundamental sinusoid and some number of component sinusoids of various frequencies (always higher than the fundamental frequency) of various amplitudes (always smaller than the that of the fundamental sinusoid). The fundamental sinusoid and the harmonic sinusoids are summed together to reconstruct the original signal. This is demonstrated as follows:
Given the following sine wave: sin(t) from 0 to 2PI

Add the third harmonic: sin(t) + 1/2 sin(3t)
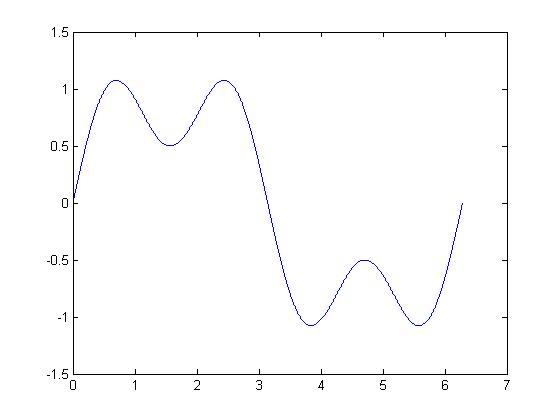
Add the fifth harmonic: sin(t) + 1/2 sin(3t) + 1/3 sin(5t)

Adding up to the 19th odd-numbered harmonic, we obtain:
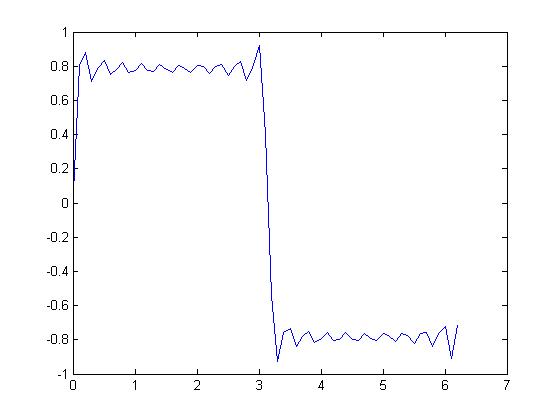
As we continue adding the odd numbered harmonics, the shape begins to look like a square wave. Notice that the ripple in the waveform has the same frequency as the highest ordered harmonic. If we continue adding the odd harmonics, we will eventually produce a "square wave":

One might ask the question, "what good is it to decompose a squarewave into component sinusoids?"...
Circuits are easily analyzed by inputting each individual (or harmonic) sine wave, and calculating the output using basic circuit analysis techniques. If the system is linear, and thankfully a vast majority are linear, we can impose the law of superposition to add the various resultant outputs together to form the result of a square wave input on the circuit. Basically, the law of superposition states that if a system is linear, the outputs which are attributed to component inputs can be added together to produce the output.
Laws like superposition make the lives of Electrical Engineers much easier.